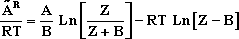Learning undergraduate engineering thermodynamics might be less painful with a blog. I hope that students, faculty and interested observers will share their thoughts on the laws of thermodynamics, phase and chemical equilibrium and many related topics.
Friday, June 01, 2007
Final Exam 2007
It has been a pleasure working with all of you. I hope you do well on the final. Remember you can use 3 8.5" x 11" cheat sheets (with writing on both sides) during the final.
We will take the class photo before the final on Monday morning. Sorry I forgot about it today. It is optional, you can choose not to be in the photo if you wish.
Best of luck in your career and in life.
Adios,
Dr. B
Tuesday, May 22, 2007
HW #9, P1 - Brayton Cycle with Variable Heat Capacities - 6 pts
HW #9, P2 - Brayton Cycle with Regeneration - 8 pts
a.) The temperature of the turbine effluent.
b.) The net work output, in kJ/kg of air flowing through the system.
c.) The thermal efficiency of the cycle.
HW #9, P3 - Effect of Turbine Feed T on Rankine Cycle Efficiency - 6 pts
a.) For T2 = 580oC, determine the quality of the turbine effluent and the thermal efficiency of the cycle.
b.) Plot the quality of the turbine effluent and the thermal efficiency of the cycle for values of T2 ranging from 580oC to 700oC at 10oC increments.
HW #9, P4 - Special Rankine Cycle with Reheat and Regeneration - 8 pts

Determine...
a.) The thermal efficiency of the cycle.
b.) The mass flow rate of water/steam through the boiler in kg/h. if the net power output of the cycle is 320 MW.
HW #9, P5 - Helium Gas Refrigeration Cycle - 6 pts
a.) The minimum temperature in the cycle.
b.) The coefficient of performance.
c.) The mass flow rate of the helium in kg/s for a refrigeration load of 12 kW.
HW #9, P6 - Ammonia Cascade Refrigeration Cycle - 8 pts

Determine...
a.) The mass flow rate of R-134a through each compressor in lbm/h.
b.) The power input to each compressor in Btu/h.
c.) The coefficient of performance of the cycle.
HW #9, P7 - Vapor-Compression Heat Pump - 6 pts
a.) The power input to the compressor in kW.
b.) The heating capacity of the heat pump in kW.
c.) The coefficient of performance.
d.) The isentropic compressor efficiency.
Monday, May 21, 2007
Test #2 - Ch 5 to 8, May 22, 2007
Monday, May 14, 2007
HW #8, P1 - Back-Work Ratio of a Steam Power Cycle - 4 pts
HW #8, P2 - Isentropic Efficiency of a CO2 Compressor - 4 pts
HW #8, P3 - Analysis of an R-134a Compressor - 5 pts
a.) The temperature of the R-134a at the outlet of the compressor.
b.) The power input to the compressor in kW.
c.) Show the process path on a TS Diagram that includes the two phase envelope and all relevant isobars.
HW #8, P4 - Polytropic Compression of N2 with Varying delta - 6 pts
a.) Isentropic, gamma = 1.4
b.) Polytropic with delta = 1.3
c.) Isothermal
d.) Ideal, two-stage polytropic with delta = 1.3
HW #8, P5 - Lost Work in a Heat Exchanger - 4 pts

a.) The exit temperature of the oil.
b.) The rate of entropy generation in the heat exchanger.
c.) The rate at which work is lost due to the irreversible nature of heat transfer in this process in kW. Assume the surroundings are at 20oC.
HW #8, P6 - Entropy Change, Heat Transfer and Irreversibilities - 3 pts
a.) Internally reversible process with Q > 0.
b.) Internally reversible process with Q = 0.
c.) Internally reversible process with Q < 0.
d.) Internal irreversibilities present with Q > 0.
e.) Internal irreversibilities present with Q = 0.
f.) Internal irreversibilities present with Q < 0.
HW #8, P6 - Entropy Change, Heat Transfer and Irreversibilities - 3 pts
a.) Internally reversible process with Q > 0.
b.) Internally reversible process with Q = 0.
c.) Internally reversible process with Q < 0.
d.) Internal irreversibilities present with Q > 0.
e.) Internal irreversibilities present with Q = 0.
f.) Internal irreversibilities present with Q < 0.
HW #8, P7 - Entropy Generation and Lost Work in a Nozzle - 5 pts
a.) For a system that encloses the nozzle only, determine the heat transfer (kJ/kg) and the change in specific entropy (kJ/kg-K), both per kg of oxygen flowing through the nozzle. What additional information would be required to evaluate the rate of entropy production in this process ?
b.) Using an enlarged system boundary that includes the nozzle and a portion of its immediate surroundings, evaluate the rate of entropy generation (kJ/kg-K) and the rate of lost work (kJ/kg), both per kg of oxygen flowing through the nozzle. Assume that heat exchange at the enlarged system boundary takes place at the ambient temperature, 20oC.
Treat O2 as an ideal gas with variable heat capacities. Verify that the ideal gas assumption is valid.
HW #8, P8 - Lost Work in an Air Compressor and HEX - 6 pts

a.) The compressor power requirement in kW and the mass flow rate of the cooling water in kg/s.
b.) The rate of entropy generation in kW/K and the rate at which work is lost in kW for the compressor. Assume the temperature of the surroundings is 300 K.
c.) The rate of entropy generation in kW/K and the rate at which work is lost in kW for the heat exchanger. Assume the temperature of the surroundings is 300 K.
Wednesday, April 25, 2007
HW #7, P1 - The Increase of Entropy Principle - 3 pts
b.) Will the entropy of the working fluid in an ideal Carnot Cycle increase, decrease or remain the same during the isothermal heat addition process ?
c.) Steam is accelerated as it flows through a real, adiabatic nozzle. Will the entropy of the steam at the nozzle exit be greater than, equal to or less than the entropy at the nozzle inlet ?
HW #7, P2 - Efficiency of an Int. Rev. HE with Multiple Heat Transfers - 4 pts
HW #7, P3 - Efficiency and Tres for Rev. and Irrev. Cycles - 6 pts
a.) Reversible and irreversible power cycles each discharge QC to a cold reservoir at TC and receive energy QH from hot reservoirs at TH and T'H, respectively. There are no other heat transfers involved. Show that T'H> TH.
b.) Reversible and irreversible refrigeration cycles each discharge QH to a hot reservoir at TH and receive energy QC from cold reservoirs at TC and T'C, respectively. There are no other heat transfers involved. Show that T'C> TC.
HW #7, P4 - ΔSSys, ΔSRes, and ΔSUniv, for a H.T. Process - 3 pts
a.) the entropy change of the working fluid
b.) the entropy change of the heat source
c.) the total entropy change of the universe for this process.
HW #7, P5 - Specific Entropy Change Using Tabluar Data - 4 pts
a.) Water: P1 = 10 MPa, T1 = 400oC and P2 = 10 MPa, T2 = 100oC.
b.) R-134a: H1 = 211.44 kJ/kg, T1 = - 40oC and P2 = 5 bar, x2 = 1.0.
c.) Air (IG): T1 = 7oC, P1 = 2 bar and T2 = 327oC, P2 = 1 bar.
d.) Hydrogen (H2, IG): T1 = 727oC, P1 = 1 bar and T2 = 25oC, P2 = 3 bar.
HW #7, P6 - "Show That" for a Cycle Interacting with Three Reservoirs - ?? pts
HW #7, P7 - Three-Step, Ideal Gas Cycle Analysis - 8 pts
Step 1 - 2 : Isothermal expansion at 250 K from 4.75 bar to 1.0 bar.
Step 2 - 3 : Adiabatic compression to 4.75 bar.
Step 3 - 1 : Isobaric cooling.
a.) Sketch the cycle on a PV diagram.
b.) Sketch the cycle on a TS diagram.
c.) Determine T3 in Kelvin
d.) If the cycle is a power cycle, determine its thermal efficiency. If the cycle is a refrigeration cycle, determine its COP.
HW #7, P8 - Entropy Change in the Evaporator of a Refrigerator - ?? pts
a.) The entropy change of the refrigerant.
b.) The entropy change of the refrigerated space.
c.) The entropy change of the universe for the process.
HW #7, P9 - Maximum Work From an Adiabatic Turbine - ?? pts
HW #7, P10 - DeltaS{Univ} Upon Quenching an Iron Block - ?? pts
HW #7, P11 - DeltaS for Heat Transfer to R-134a in a Rigid Tank - ?? pts
a.) The entropy change of the R-134a.
b.) The entropy change of the heat source.
c.)The entropy change of the universe for this process.
Tuesday, April 24, 2007
HW #6, P1 - "Show That" Using the K-P Statement of the 2nd Law - 6 pts
a.) The coefficient of performance (COP) of an irreversible heat pump cycle is always less than the COP of a reversible heat pump when both heat pumps exchange heat with the same two thermal reservoirs.
b.) All reversible heat pump cycles exchanging heat with the same two thermal reservoirs have the same COP.
HW #6, P2 - Rev., Irrev. and Impossible Refrigeration Cycles - 8 pts
a.) QC = 1000 kJ and Wcycle = 400 kJ
b.) QC = 1500 kJ and QH = 1800 kJ
c.) QH = 1500 kJ and Wcycle = 200 kJ
d.) COP = 4
HW #6, P3 - A Reversible HE Used to Drive a Reversible Heat Pump - 6 pts
HW #6, P4 - Effect of Source and Sink Temperatures on HE Efficiency - 6 pts
HW #6, P5 - Maximum Efficiency of a Geothermal Power Plant - 2 pts
HW #6, P6 - Carnot Gas Power Cycle Analysis - 8 pts
a.) The maximum and mininmum temperatures for the cycle in Kelvin.
b.) The pressure in bar and volume in m3 at the beginning of the isothermal expansion.
c.) The work and heat transfer for each of the four processes in kJ.
Assume: CV,air = 0.731 kJ/kg-K (constant).
d.) Sketch the cycle on a PV diagram.
HW #6, P7 - Carnot HE Used to Drive a Carnot Refrigerator - 6 pts
a.) the maximum rate of heat removal from the refrigerated space
b.) the total rate of heat rejection to the ambient air
HW #6, P8 - Ammonia Carnot Vapor Refrigeration Cycle - 10 pts
a.) Sketch the cycle on a PV diagram.
b.) Evaluate the heat and work for each process in kJ.
c.) Evaluate the COP for this cycle.
Sunday, April 15, 2007
HW #5, P1 - Adiabatic Steam Nozzle - 5 pts
a.) The temperature of the steam when it leaves the nozzle.
b.) The ratio of the inlet cross-sectional area to the outlet cross-sectional area, A1 / A2.
Assume the process operates at steady-state.
HW #5, P2 - Adiabatic Gas Turbine - 5 pts
HW #5, P3 - Effluent Pressure in a Non-Adiabatic Steam Diffuser - 6 pts
HW #5, P4 - Analysis of a Two-Stage, Adiabatic Turbine - 6 pts
a.) The mass flow rate of the steam at each of the two exits.
b.) The diameter in meters of the duct through which the 0.5 MPa steam is extracted if the velocity there is 20 m/s.

HW #5, P5 - Analysis of an Adiabatic Steam De-Superheater - 6 pts
a.) If T3 = 200oC, determine the mass flow rate of stream 3.
b.) Plot the mass flow rate of stream 3 in kg/s as a function of T3 as T3 ranges from 20 to 220oC.

HW #5, P6 - Pump Horsepower Requirment - 6 pts

HW #5, P7 - Waste Heat Steam Generator - 6 pts
CP,air = 7.05 Btu/lbmole-oF.

HW #5, P8 - Transient Heating of an Office Space - 7 pts
HINTS :
This is a transient or unsteady process because helium enters the system (the balloon). Assume the He behaves as an ideal gas, but check to see if this is a good assumption. Use the IG EOS to determine the initial mass of He in the balloon. After you determine V2, calculating Wb is easy ! Then, simultaneously solve two equations in two unknowns. The equations are: the IG EOS applied to the final state of the balloon and the transient form of the 1st Law applied to this process. The two unknowns are: T2, mHe,2 .
The catch is that we must determine values for U1, U2 and Hin. These are NOT ΔU's and ΔH's but real U's and H's. In order to do this (just like the steam tables) we MUST choose a reference state. A reference state is a T, P and phase at which YOU choose to make EITHER U or H zero kJ/kg. I want you to use a reference state of U = 0 for He gas at 22 oC and 100 kPa. The P doesn't actually matter because He is treated as an IG in this problem so U and H are not functions of P anyway.
Once you have a ref state, use a Hypothetical Process Path from the ref state to states 1, 2 and inlet to evaluate U1, U2 and Hin using the IG EOS and CV and CP given in the problem.
For He, use: CP = 5.1926 kJ/kg-K and CV = 3.1156 kJ/kg-K.
HW #5, P9 - Filling a Balloon with Helium - 10 pts
This is a transient or unsteady process because helium enters the system (the balloon). Assume the He behaves as an ideal gas, but check to see if this is a good assumption. Use the IG EOS to determine the initial mass of He in the balloon. After you determine V2, calculating Wb is easy ! Then, simultaneously solve two equations in two unknowns. The equations are: the IG EOS applied to the final state of the balloon and the transient form of the 1st Law applied to this process. The two unknowns are: T2, mHe,2 .
The catch is that we must determine values for U1, U2 and Hin. These are NOT ΔU's and ΔH's but real U's and H's. In order to do this (just like the steam tables) we MUST choose a reference state. A reference state is a T, P and phase at which YOU choose to make EITHER U or H zero kJ/kg. I want you to use a reference state of U = 0 for He gas at 22 oC and 100 kPa. The P doesn't actually matter because He is treated as an IG in this problem so U and H are not functions of P anyway.
Once you have a ref state, use a Hypothetical Process Path from the ref state to states 1, 2 and inlet to evaluate U1, U2 and Hin using the IG EOS and CV and CP given in the problem.
For He, use: CP = 5.1926 kJ/kg-K and CV = 3.1156 kJ/kg-K.
Test #1
Wednesday, April 11, 2007
HW #4, P1 - Compression of Cooling Air by a Linear Spring - 6 pts

HW #4, P2 - Work and Heat Transfer for a Closed, 3-Step Cycle - 6 pts
Process 1 - 2: Adiabatic compression from P1 = 50 psia, V1 = 3.0 ft3 to V2 = 1 ft3 along a path described by :

Process 2 - 3: Constant volume.
Process 3 - 1: Constant pressure with U1 - U3 = 46.7 Btu.
There are no significant changes in kinetic or potential energies in any of these processes.
a.) Sketch this cycle on a PV Diagram.
b.) Calculate the net work for the cycle in Btu.
c.) Calculate the heat transfer for process 2-3.
HW #4, P3 - Heat Conduction Through a Composite Wall - 4 pts
Brick Insulation
Data : k 1.4 0.05 Btu/h-ft2-oR
HW #4, P4 - Combined Convection and Radiation Heat Loss - 4 pts
HW #4, P5 - Minimum Insulation Thickness for a Hot Surface - 5 pts
HW #4, P6 - Isobaric Expansion of R-134a - 6 pts

a.) The temperature of the R-134a when the piston reaches the stops.
b.) The boundary work done during this expansion process.
c.) The heat transfer during this expansion process.
d.) Show this process on a PV Diagram.
HW #4, P7 - 1st Law Analysis of Steam in a Closed System - 4 pts

HW #4, P8 - Power Plant Efficiency - 3 pts
a.) Determine the net rate at which power is developed in MW.
b.) For 8000 hours of operation annually, determine the net work output in kW-h/yr.
c.) Evaluating the net work output at $0.08 per kW-h, determine the value of the net work in $/yr.
HW #4, P9 - Work, Heat and COP in a Refrigeration Cycle - 2 pts
HW #4, P10 - Heat Pump COP and Monthly Operating Cost - 2 pts
a.) Determine the net power required to operate the heat pump in kW.
b.) Evaluating electricity at $0.08 per kW-h, determine the cost of electricity in a month when the heat pump operates for 200 hours.
Thursday, April 05, 2007
Ch 3 - Anything Except HW
Dr. B
HW #3, P1 - Steam NIST / TFT Fundamentals - 2 pts
T (oC) P (kPa) H (kJ/kg) x (kg vap/kg) Phase Description
a.) P = 200 kPa, x = 0.7 kg vap/kg
b.) T = 140oC , H = 1800 kJ/kg
c.) P = 950 kPa, x = 0 kg vap/kg
d.) T = 80oC, P = 500 kPa
e.) P = 800 kPa, H = 3161.7 kJ/kg
HW #3, P2 - R-134a NIST/TFT Fundamentals - 2 pts
T(oF) P(psia) U(Btu/lbm) x(lbm vap/lbm) Phase Description
a.) P = 80 psia, U = 126 Btu/lbm
b.) T = 15oF, x = 0.6 lbm vap/lbm
c.) T = 10oF, P = 70 psia
d.) P = 180 psia, U = 224 Btu/lbm
e.) T = 110oF, x = 1.0 lbm vap/lbm
HW #3, P3 - Determining DH Using Heat Capacity Polynomials - 6 pts
a.) The empirical specific heat equation (Shomate Equation) from the NIST Website.
b.) "The CoV value at the average temperature.
(Use the heat capacity polynomial to determine this CoV value.)
c.) The CoV value at room temperature, 25oC.
(Use the heat capacity polynomial to determine this CoV value.)
HW #3, P4 - Determining DU Using Heat Capacity Polynomials - 6 pts
a.) The empirical specific heat equation (Shomate Equation) from the NIST Website.
b.) The CoV value at the average temperature.
(Use the heat capacity polynomial to determine this CoV value.)
c.) The CoV value at room temperature, 25oC.
(Use the heat capacity polynomial to determine this CoV value.)
HW #3, P5 - Clapeyron & Clausius-Clapeyron Equations - 6 pts
a.) The Clapeyron Equation
b.) The Clausius-Clapeyron Equation
c.) The ammonia tables
HW #3, P6 - Hypothetical Process Paths and the Latent Heat of Vaporization - 8 pts
Assume heptane gas is an ideal gas at the relevant temperatures and pressures.

Tuesday, March 27, 2007
Ch 2 - Any thing except HW
Dr. B
Ch 1 - Any thing except HW
Dr. B
Wednesday, March 21, 2007
HW #2, P1- Steam Table Fundamentals - 4 pts
Dr. B
HW #2, P2- R-134a Table Fundamentals - 4 pts
Dr. B
HW #2, P3- R-134a Table Fundamentals - 4 pts
Dr. B
HW #2, P4- Isochoric Heating of Water - 4 pts
Dr. B
HW #2, P5- Isobaric Expansion of Water - 6 pts
Dr. B
HW #2, P6- Inflating an Automobile Tire - 6 pts
Dr. B
HW #2, P7- An Application of Equations of State - 8 pts
Dr. B
HW #2, P8- Relative Humidity and Fogged Glasses - 5 pts
Dr. B
HW #2, P9- Spray Dryer - 5 pts
Dr. B
HW #1, P1- Mass, Force, Density and Acceleration - 4 pts
Dr. B
HW #1, P2- Mass, Weight and Acceleration - 3 pts
Dr. B
HW #1, P3- NOx Emissions: UNITS - 3 pts
Dr. B
HW #1, P4- Temperature Conversions: Celsius to Fahrenheit - 2 pts
Dr. B
HW #1, P5- Temperature Conversions: Fahrenheit to Celsius - 2 pts
Dr. B
HW #1, P6- Temperature Change - 2 pts
Dr. B
HW #1, P7- Absolute and gauge Pressures - 5 pts
Dr. B
HW #1, P8- Differential, Multi-Fluid Manometer - 6 pts
Dr. B
Saturday, March 10, 2007
Final Exam
It has been a pleasure working with you.
Best of luck on the final exam !
Adios,
Dr. B
Friday, March 02, 2007
HW #6, P13.34 - Multiple Reaction Equilibria and Their Dependence on T and P - 22 pts

The only other reaction considered is :

Assume equilibrium is attained for both reactions at 1 bar and 1300 K.
a.) Would it be better to carry out the reaction at pressures above 1 bar ?
b.) Would it be better to carry out the reaction at temperatures below 1300 K ?
c.) Estimate the molar ratio of H2 to CO in the synthesis gas if the feed consists of an equimolar mixture of steam and methane,
d.) Repeat part c) for a steam to methane mole ratio in the feed of 2.0.
e.) How could the feed composition be altered to yield a lower ratio of H2 to CO in the synthesis gas than is obtained in part c.) ?
f.) Is there any danger that carbon will deposit by the reaction :
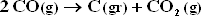
under conditions of part (c) ? Part d ? If so, how could the feed be altered to prevent carbon deposition ?
HW #6, P13.31 - Keq and γi for a Liquid Phase Isomerization Reaction - 10 pts

where A and B are miscible liquids for which :

If ΔGo298 = -1,000 J/mole, what is the equilibrium composition of the mixture at 25oC ? How much error is introduced if one assumes that A and B form an ideal solution ?
HW #6, P13.24 - Independent Chemical Reactions and Degrees of Freedom - 4 pts
HW #6, P13.23 - Vapor Pressure of Decompositioon of NH4Cl(s) to NH3 and HCl - 12 pts
HW #6, P13.20 - Eeq as a Funtion of Temperature for Ammonia Synthesis from N2 and H2 - 14 pts

The equilibrium conversion to ammonia is large at 300 K, but decreases rapidly with increasing T. However, reaction rates become appreciable only at higher temperatures. For a feed mixture of hydrogen and nitrogen in stoichiometric proportion :
a.) What is the equlibrium mole fraction of ammonia at 1 bar and 300 K ?
b.) At what temperature does the equilibrium mole fraction of ammonia equal 0.5 for a pressure of 1 bar ?
c.) At what temperature does the equilibrium mole fraction of ammonia equal 0.5 for a pressure of 100 bar, assuming the equilibrium mixture is an ideal gas ?
d.) At what temperature does the equilibrium mole fraction of ammonia equal 0.5 for a pressure of 100 bar, assuming the equilibrium mixture is an ideal solution of gases ?
HW #6, P13.15 - Isothermal Operation of an SO2 Catalytic Converter - 12 pts
HW #6, P13.13 - Effect of Pressure Change on Eeq of Reaction for the Hydrogenation of Acetaldehyde - 10 pts

If the system initially contains 1.5 mol H2 for each mole of acetaldehyde, what is the composition of the system at equilibrium ? What would be the effect of reducing the pressure to 1 bar ? Assume ideal gas behavior.
HW #6, P13.5c - Problem title here - 6 pts

At high temperatures and low to moderate pressures, the reacting species form an ideal gas mixture. Application of the summability equation to Eq. (11.26) yields :

When the Gibbs energies of the elements in their standard states are set equal to zero, Gi = DGof,i for each species, and then :

At the beginning of Sec. 13.2, we noted that Eq. (14.64) is a criterion of equilibrium. Applied to the water-gas-shift reaction with the understanding that T and P are constant, this equation becomes :

Here, however, dn/dε = 0. The equilibrium criterion therefore becomes:

Once the yi are eliminated in favor of ε, Eq. (A) relates G to ε. Data for ΔGof,I for the compounds of interest are given with Ex 13.13. For a temperature of 1300 K (the reaction is unaffected by P) and for a feed of 1 mol H2 and 1 mol CO2:
a.) Determine the equilibrium value of ε by application of Eq. (B).
b.) Plot G vs. ε, indicating the location of the equilibrium value of ε determined in part (a).
Sunday, February 18, 2007
Test #2 - SVN Chapters 11 & 12
Best of luck on Tuesday !
Thursday, February 15, 2007
HW #5, P12.3 - Fitting VLE Data Using the Margules, van Laar & Wilson Equations - 18 pts
P (kPa) x1 y1 P (kPa) x1 y1 P (kPa) x1 y1
68.728 0.0000 0.0000 93.206 0.3579 0.4779 100.278 0.6945 0.7124
72.278 0.0287 0.0647 95.017 0.405 0.5135 100.467 0.7327 0.7383
75.279 0.0570 0.1295 96.365 0.448 0.5512 100.999 0.7752 0.7729
77.524 0.0858 0.1848 97.646 0.5052 0.5844 101.059 0.7922 0.7876
78.951 0.1046 0.2190 98.462 0.5432 0.6174 99.877 0.9080 0.8959
82.528 0.1452 0.2694 99.811 0.6332 0.6772 99.799 0.9448 0.9336
86.762 0.2173 0.3633 99.950 0.6605 0.6926 96.885 1.0000 1.0000
90.088 0.2787 0.4184
d.) Basing calculations on the Modified Raoult's Law, find parameters for the margules Equation that provide the best fit of GE/RT to the data and prepare a Pxy Diagram that compares the experimental points with curves determined from the correlation.
e.) Repeat part (c) for the van Laar Equation.
f.) Repeat part (c) for the Wilson Equation.
HW #5, WB.1 - Pxy Diagram and Henry's Law Constants for Dichloromethane and Methanol - 14 pts
a.) Make a Pxy Diagram in Excel based on this data. No curve fit is necessary. Describe any unusual features in this diagram. Be specific and quantitative in your description.
b.) Make a fugacity or partial pressure plot (plot y1 P vs x1 and y2 P vs x1 on the same figure) in Excel. SVN Figure 12.2 is an example of such a plot.
c.) Determine the Henry's Law Constant at 50oC for each species from the partial pressure curves constructed in part b. Draw a line on each graph from part b, by hand or using Excel's drawing tools, that shows the graphical interpretation of the Henry's Law Constant for each species. (Ans.: Low-tech method (use last 2 data points and draw a line): k2 = 334 kPa/(mole 2/mol), High-tech method (fit the last 3 data points to a quadratic eqn and determine the slope as xi approaches 0): k2 = 437 kPa/(mole 2/mol) )
d.) Estimate the range of x1 values over which H1 is applicable and the range of x2 values over which H2 is applicable. Consider H values applicable as long as the error incurred is less than 5% of the partial pressure of the species.
Data :
P (kPa) x1 y1
55.55 0.000 0.000
58.79 0.042 0.093
61.76 0.097 0.174
64.59 0.189 0.265
65.66 0.292 0.324
65.76 0.349 0.349
65.59 0.415 0.367
65.15 0.493 0.386
63.86 0.632 0.418
62.36 0.720 0.438
59.03 0.835 0.484
54.92 0.893 0.537
48.41 0.945 0.620
31.10 1.000 1.000
HW #5, WB.2 - Determination of Azeotropes Using Margules and van Laar Equations - 12 pts
a.) Benzene(1) / acetonitrile(2) at 40oC. Margules parameters: A12 = 1.780, A21 = 1.055. Vapor pressures at 40oC: P1* = 29.82 kPa, P2* = 22.78 kPa.
Ans.: P ≈ 37 kPa
b.) Acetone(1) / chloroform(2) at 50oC. van Laar parameters: L12 = -0.936, L21 = -0.678. Vapor pressures at 50oC: P1* = 81.75 kPa, P2* = 69.38 kPa.
Ans.: P ≈ 61 kPa
Hints :
How can you recognize when an azeotrope exists ? Express this idea in terms of the Modified raoult's law and the Margules and van Laar Equations.
Monday, February 12, 2007
HW #5, WB.3 - Determination of Azeotropes Using the Wilson Equation - 8 pts
HW #5, WB.4 - Bubble Point and Dew Point Calculations Using the Wilson Equation - 22 pts
Ln[P1*] = 16.5938 - 3644.30 / ( t + 239.76 )
Ln[P2*] = 14.7258 - 3271.24 / ( t + 241.85 )
Where P* is in kPa and t is in oC.
a.) Calculate Pbub, given x1 = 0.73 and T = 70oC
b.) Calculate Tdew, given y1 = 0.63 and P = 101.325 kPa
HW #5, P12.22 - Multicomponent Flash Using the Wilson Equation - 20 pts
a.) Bubble point temperature for P = 101.33 kPa, x1 = 0.30 and x2 = 0.40.
b.) Dew point temperature for P = 101.33 kPa, y1 = 0.30 and y2 = 0.40.
c.) PT Flash: Given P = 101.33 kPa, T = (Tbub+Tdew)/2, and z1 = 0.30 and z2 = 0.20.
HW #5, P12.27 - Volume Change of Mixing Two Liquids - 6 pts

Given that V1 = 58.63 cm3/mol and V2 = 118.46 cm3/mol, what volume of mixture is formed when 750 cm3 of pure species 1 is mixed with 1500 cm3 of pure species 2 at 25oC ? What would be the volume of the mixture if an ideal solution were formed ?
Wednesday, February 07, 2007
HW #4, P11.25 - Fugacity of a Mixture: Real vs. Ideal Solution - 8 pts
a.) Through application of Eqs.(11.59) and (11.60).
(Actually, use the SRK EOS, like in class.)
b.) Assuming that the mixture is an ideal solution.
HW #4, P10.25+ - Bubble and Dew Point Calculations Using the SRK EOS - 16 pts
a.) Pbub, given x1 = 0.10, x2 = 0.50 and t = -60oF.
b.) Pdew, given y1 = 0.50, y2 = 0.25 and t = -60oF.
c.) Tbub, given x1 = 0.12, x2 = 0.40 and P = 250 psia.
d.) Tdew, given y1 = 0.43, y2 = 0.36 and P = 250 psia.
Hints:
Do parts b and c only.
Use the results from my solution to this problem in HW#2, based on the DePriester Charts, as a starting point for SRK.
Use the SRK equations for mixtures to answer this question. The equations are the 2 SRK eqns in terms of Zliq and Zvap and three equilibrium eqns. The unknowns are The two Z's, two of the three yi's and the total pressure.
You will need to run Solver several times, tweaking your guesstimates of the unknown variables each time, in order to get Excel to converge to the correct answer. The correct answer is the one that yields the lowest value of the Σerror^2.
HW #4, P10.31+ - Equilibrium Flash Distillation Using the SRK EOS - 20 pts
Hints:
Use the results from my solution to this problem in HW#2, based on the DePriester Charts, as a starting point for SRK. Solve for P, the 4 xi's, the 4 yi's and the two Z's (compressibility of the vapor and liquid phases). That is a whopping 11 unks. I reduced the problem to 9 unks by forcing the Σxi = 1 and Σyi = 1. The 9 eqns include 3 independent material balance eqns, 4 equilibrium eqns and 2 SRK eqns in terms of two Z's, A's and B's. Remember that A, B and Z are not the same in the liquid phase as they are in the vapor phase.
HW #4, P11.28 - Excess Gibbs Free Energy of a Real Liquid Mixture - 16 pts
a.) Find expressions for Ln g1 and Ln g2 at T and P.
b.) Show that when these expressions are combined in accord with Eq.(11.95) the given equation for GE/RT is recovered.
c.) Show that these expressions satisfy Eq.(11.96), the Gibbs/Duhem Equation.
d.) Show that (d Ln g1 / dx1)x1=1 = (d Ln g2 / dx1)x1=0 = 0.
e.) Plot GE/RT, Ln g1 and Ln g2 as calculated by the given equation for GE/RT and by the equations developed in part (a) vs. x1. Label points Ln g1∞ and Ln g2∞ and show their values.
HW #4, P11.36 - Excess Gibbs Free Energy of a Real Liquid Mixture - 12 pts
a.) Determine from the data numerical values of parameters a, b and c in the correlating equation:

b.) Determine from the results of part (a) the minimum value of HE. At what value of x1 does this occur ?
c.) Determine from the results of part (a) expressions for : partial molar HE1 and partial molar HE1. Prepare a plot of these quantities vs. x1 and discuss its features.
x1 HE~ (J/mol)
0.0426 -23.3
0.0817 -45.7
0.1177 -66.5
0.1510 -86.6
0.2107 -118.2
0.2624 -144.6
0.3472 -176.6
0.4158 -195.7
0.5163 -204.2
0.6156 -191.7
0.6810 -174.1
0.7621 -141.0
0.8181 -116.8
0.8650 -85.6
0.9276 -43.5
0.9624 -22.6
Saturday, January 20, 2007
ChemE 326 - Test #1
HW #3, P11.2 - Entropy Change of Mixing - 10 pts
Hints :
Calculate ΔS for each step of a hypothetical process path.
First convert N2 from the initial to the final state. Then, change Ar from the initial to the final state. Finally, mix the N2 and the Ar at the final T and P.
Ans.: ΔS ≈ 38 J/K
HW #3, WB-1 - A Perpetual Motion Machine of the Second Kind - 12 pts
Hints :
The first step in the analysis of this process is to solve the material and energy balance equations. The more subtle part is to calculate ΔS for the process. I broke the process into a hypothetical process path consisting of seven steps. Three of these steps consist of mixing pure He and CH4 at constant T and P while the remaining four steps involved changes in T or P for either pure He or CH4.
HW #3, P11.8 - Partial Molar Volumes of the Components of a Binary Mixture - 6 pts
1/V~ = a0 + a1 x1 + a2 (x1)^2
find the corresponding expressions for Vbar1 and Vbar2.
Hints :
Use equations 11.15 and 11.16.
The xi's are mole fractions of species i.
HW #3, P11.13 - Partial Molar Volumes and the Gibbs-Duhem Equation - 10 pts
V~ = 120 x1 + 70 x2 + (15 x1 + 8 x2) x1 x2
a.) Find expressions for the partial molar volumes of species 1 and 2 at T and P.
b.) Show that when these expressions are combined in accord with Eqn 11.11 the given equation for V~ is recovered.
c.) Show that these expressions satisfy Eqn 11.14, the Gibbs-Duhem equation.
d.) Show that at constant T and P,
(dVbar1/dx1)@x1=1 = (dVbar2/dx1)@x1=0 = 0
e.) Plot values of V~, Vbar1, and Vbar2 calculated by the given equation for V~ and by the equations developed in part (a) vs. x1. Label points V~1, V~2, Vbar1 at infinite dilution and Vbar2 at infinite dilution.
Hints :
a.) This is similar to 11.8 Ans.: V2 = 14 x13 + x12 + 70
b.) Just a little bit of algebra here. Ans.: V = -7 x13 - x12 + 58 x1 + 70
c.) A bit of algebra with just a touch of differential calculus.
d.) Just a couple of derivatives and some plug-n-chug.
e.) A snap for you and your friend, Excel.
HW #3, P11.23b - Fugacity of Subcooled Liquid Isobutylene - 8 pts
Use the SRK EOS to determine the fugacity coefficient of saturated liquid isobutylene at TNBP. Then, use the SRK EOS to estimate the molar volume of saturated liquid isobutylene at TNBP.
HW #3, P11.24b - Fugacity and Fugacity Coefficient of Isobutane as Functions of Pressure - 12 pts
Use the SRK EOS to determine the fugacity coefficient of saturated vapor/liquid isobutane. You can also use SRK to calculate the fugacity coefficient of superheated vapors directly. Then, it is relatively easy to calculate the fugacity of the superheated vapors. Subcooled liquids require the use of SRK and the Poynting Factor. Then, use the SRK EOS to estimate the molar volume of saturated liquid isobutane.
Plot 21 data points from 0 to 10 bar, every 0.5 bar. This will entail using Solver for each data point. Remember to completely label your plots.
Monday, January 01, 2007
Welcome to the ChemE Thermo Blog !
You can come here and click the phrase "# comments" and post your questions on the appropriate HW problem. The "#" part is the number of comments that have already been posted on each Blog entry. Try it out. Post a comment on this Blog entry just for grins.
When you post a comment on a Blog entry, you must choose an identity. Please choose "Other" and make up a screen name. Please do NOT choose "anonymous". Nobody will know who you are from your screen name.
I hope you find the Blog as helpful as other students have. It is more efficient than me answering individual email questions.
Enjoy the quarter !
HW #1, 6.1 - Slope and Curvature of Isobars on a Mollier Diagram - 4 pts
HW #1, 6.2 - Exactness of Differentials of State Variables - 8 pts

What is the result of application of this equation to an ideal gas ?
b.) Heat capacities CP and CV are defined as temperature derivatives respectively of U and H. Because these properties are realted, one expects the heat capacities also to be related. Show that the general expression connecting CP to CV is:

Show that equation B of example 6.2 is another form of this expression.
HW #1, 6.41 - Problem title here- 8 pts
Starting from Eqn (*) in the class handout from lecture #3,
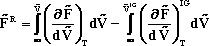
derive the equation for the Helmholtz Free Energy in Eqn (**) of the same handout.
Show all your work and explain every step of the derivation.
HW #1, 6.49 - Enthalpy and Entropy Changes of Vaporization - 12 pts
a.) Determine values for Gliq and Gvap for saturated liquid and vapor at 150 psia. Should these be the same ?
b.) Determine values for DHvap / T and DSvap at 150 psia. Should these be the same ?
c.) Find values for VR, HR, and SR for saturated vapor at 150 psia.
d.) Estimate a value for dP*/dT at 150 psia and apply the Clapeyron Equation to evaluate DSvap at 150 psia. Does this result agree with the steam table value ?
e.) Use the SRK EOS to evaluate VR, HR, and SR for saturated vapor at 150 psia. Do these results agree with the values you found in part [c] ?
HW #1, 6.54 - Enthalpy, Entropy and Molar Volume of Ideal Gases - 12 pts
HW #1, WB.2 - Production of Acetylene from Calcium Carbide and Water - 15 pts
CaC2(s) + 2 H2O(l) => C2H2(g) + Ca(OH)2(s)
Initial conditions are 25oC and 1 bar, and the reaction goes to completion. For a final temperature of 125oC, determine
a.) The final pressure
b.) The heat transferred
At 125oC, the molar volume of Ca(OH)2 is 33.0 mL/mol. Ignore the effect of any gas present in the vessel initially.
HW #1, 6.62 - Real and Ideal Work from the Isentropic Expansion of Ethane in a Turbine - 12 pts
a.) The ideal gas EOS
b.) The SRK EOS