Learning undergraduate engineering thermodynamics might be less painful with a blog. I hope that students, faculty and interested observers will share their thoughts on the laws of thermodynamics, phase and chemical equilibrium and many related topics.
Saturday, January 20, 2007
ChemE 326 - Test #1
If you have any questions related to the first test, please post them here instead of using email.
HW #3, P11.2 - Entropy Change of Mixing - 10 pts
A vessel divided into two parts by a partition, contains 4 moles of nitrogen gas at 75 degC and 30 bar on one side and 2.5 moles of argon gas at 130 degC and 20 bar on the other. If the partition is removed and the gases mix adiabatically and completely, what is the change in entropy ? Assume nitrogen to be an ideal gas with Cv = (5/2)R and argon to be an ideal gas with Cv = (3/2)R
Hints :
Calculate ΔS for each step of a hypothetical process path.
First convert N2 from the initial to the final state. Then, change Ar from the initial to the final state. Finally, mix the N2 and the Ar at the final T and P.
Ans.: ΔS ≈ 38 J/K
Hints :
Calculate ΔS for each step of a hypothetical process path.
First convert N2 from the initial to the final state. Then, change Ar from the initial to the final state. Finally, mix the N2 and the Ar at the final T and P.
Ans.: ΔS ≈ 38 J/K
HW #3, WB-1 - A Perpetual Motion Machine of the Second Kind - 12 pts
A design for purifying helium consists of an adiabatic process that splits a helium stream containing 30 mole% methane into two product steams, one containing 97 mole% helium and the other containing 90 mole% methane. The feed enters the process at 10 bar and 117oC. The methane-rich product leaves at 1 bar and 27oC while the helium-rich product leaves at 50oC and 15 bar. The process produces work! Assuming He is an ideal gas with CP = (5/2) R and methane is an ideal gas with CP = (9/2) R, calculate the total entropy change of the universe for the process on the basis of 1 mole of feed in order to determine whether the process violates the 2nd Law.
Hints :
The first step in the analysis of this process is to solve the material and energy balance equations. The more subtle part is to calculate ΔS for the process. I broke the process into a hypothetical process path consisting of seven steps. Three of these steps consist of mixing pure He and CH4 at constant T and P while the remaining four steps involved changes in T or P for either pure He or CH4.
Hints :
The first step in the analysis of this process is to solve the material and energy balance equations. The more subtle part is to calculate ΔS for the process. I broke the process into a hypothetical process path consisting of seven steps. Three of these steps consist of mixing pure He and CH4 at constant T and P while the remaining four steps involved changes in T or P for either pure He or CH4.
HW #3, P11.8 - Partial Molar Volumes of the Components of a Binary Mixture - 6 pts
If the molar density of a binary mixture is given by the empirical expression:
1/V~ = a0 + a1 x1 + a2 (x1)^2
find the corresponding expressions for Vbar1 and Vbar2.
Hints :
Use equations 11.15 and 11.16.
The xi's are mole fractions of species i.
1/V~ = a0 + a1 x1 + a2 (x1)^2
find the corresponding expressions for Vbar1 and Vbar2.
Hints :
Use equations 11.15 and 11.16.
The xi's are mole fractions of species i.
HW #3, P11.13 - Partial Molar Volumes and the Gibbs-Duhem Equation - 10 pts
The molar volume in cm^3/mol of a binary liquid mixture at T and P is given by:
V~ = 120 x1 + 70 x2 + (15 x1 + 8 x2) x1 x2
a.) Find expressions for the partial molar volumes of species 1 and 2 at T and P.
b.) Show that when these expressions are combined in accord with Eqn 11.11 the given equation for V~ is recovered.
c.) Show that these expressions satisfy Eqn 11.14, the Gibbs-Duhem equation.
d.) Show that at constant T and P,
(dVbar1/dx1)@x1=1 = (dVbar2/dx1)@x1=0 = 0
e.) Plot values of V~, Vbar1, and Vbar2 calculated by the given equation for V~ and by the equations developed in part (a) vs. x1. Label points V~1, V~2, Vbar1 at infinite dilution and Vbar2 at infinite dilution.
Hints :
a.) This is similar to 11.8 Ans.: V2 = 14 x13 + x12 + 70
b.) Just a little bit of algebra here. Ans.: V = -7 x13 - x12 + 58 x1 + 70
c.) A bit of algebra with just a touch of differential calculus.
d.) Just a couple of derivatives and some plug-n-chug.
e.) A snap for you and your friend, Excel.
V~ = 120 x1 + 70 x2 + (15 x1 + 8 x2) x1 x2
a.) Find expressions for the partial molar volumes of species 1 and 2 at T and P.
b.) Show that when these expressions are combined in accord with Eqn 11.11 the given equation for V~ is recovered.
c.) Show that these expressions satisfy Eqn 11.14, the Gibbs-Duhem equation.
d.) Show that at constant T and P,
(dVbar1/dx1)@x1=1 = (dVbar2/dx1)@x1=0 = 0
e.) Plot values of V~, Vbar1, and Vbar2 calculated by the given equation for V~ and by the equations developed in part (a) vs. x1. Label points V~1, V~2, Vbar1 at infinite dilution and Vbar2 at infinite dilution.
Hints :
a.) This is similar to 11.8 Ans.: V2 = 14 x13 + x12 + 70
b.) Just a little bit of algebra here. Ans.: V = -7 x13 - x12 + 58 x1 + 70
c.) A bit of algebra with just a touch of differential calculus.
d.) Just a couple of derivatives and some plug-n-chug.
e.) A snap for you and your friend, Excel.
HW #3, P11.23b - Fugacity of Subcooled Liquid Isobutylene - 8 pts
Estimate the fugacity of isobutylene liquid at its normal boiling point temperature and 200 bar.
Use the SRK EOS to determine the fugacity coefficient of saturated liquid isobutylene at TNBP. Then, use the SRK EOS to estimate the molar volume of saturated liquid isobutylene at TNBP.
Use the SRK EOS to determine the fugacity coefficient of saturated liquid isobutylene at TNBP. Then, use the SRK EOS to estimate the molar volume of saturated liquid isobutylene at TNBP.
HW #3, P11.24b - Fugacity and Fugacity Coefficient of Isobutane as Functions of Pressure - 12 pts
Prepare plots of f vs. P and phi vs. P for isobutane at 40 degC. Use a pressure range 0 to 10 bar. At 40 degC, the vapor pressure of isobutane is 5.28 bar.
Use the SRK EOS to determine the fugacity coefficient of saturated vapor/liquid isobutane. You can also use SRK to calculate the fugacity coefficient of superheated vapors directly. Then, it is relatively easy to calculate the fugacity of the superheated vapors. Subcooled liquids require the use of SRK and the Poynting Factor. Then, use the SRK EOS to estimate the molar volume of saturated liquid isobutane.
Plot 21 data points from 0 to 10 bar, every 0.5 bar. This will entail using Solver for each data point. Remember to completely label your plots.
Use the SRK EOS to determine the fugacity coefficient of saturated vapor/liquid isobutane. You can also use SRK to calculate the fugacity coefficient of superheated vapors directly. Then, it is relatively easy to calculate the fugacity of the superheated vapors. Subcooled liquids require the use of SRK and the Poynting Factor. Then, use the SRK EOS to estimate the molar volume of saturated liquid isobutane.
Plot 21 data points from 0 to 10 bar, every 0.5 bar. This will entail using Solver for each data point. Remember to completely label your plots.
Monday, January 01, 2007
Welcome to the ChemE Thermo Blog !
For each HW assignment and each test, I will post a message to this blog.
You can come here and click the phrase "# comments" and post your questions on the appropriate HW problem. The "#" part is the number of comments that have already been posted on each Blog entry. Try it out. Post a comment on this Blog entry just for grins.
When you post a comment on a Blog entry, you must choose an identity. Please choose "Other" and make up a screen name. Please do NOT choose "anonymous". Nobody will know who you are from your screen name.
I hope you find the Blog as helpful as other students have. It is more efficient than me answering individual email questions.
Enjoy the quarter !
You can come here and click the phrase "# comments" and post your questions on the appropriate HW problem. The "#" part is the number of comments that have already been posted on each Blog entry. Try it out. Post a comment on this Blog entry just for grins.
When you post a comment on a Blog entry, you must choose an identity. Please choose "Other" and make up a screen name. Please do NOT choose "anonymous". Nobody will know who you are from your screen name.
I hope you find the Blog as helpful as other students have. It is more efficient than me answering individual email questions.
Enjoy the quarter !
HW #1, 6.1 - Slope and Curvature of Isobars on a Mollier Diagram - 4 pts
Starting with equation 6.8, show that isobars in the vapor region of a Mollier (HS) Diagram must have positive slope and positive curvature.
HW #1, 6.2 - Exactness of Differentials of State Variables - 8 pts
a.) Making use of the fact that equation 6.20 is an exact differential expression, show that:

What is the result of application of this equation to an ideal gas ?
b.) Heat capacities CP and CV are defined as temperature derivatives respectively of U and H. Because these properties are realted, one expects the heat capacities also to be related. Show that the general expression connecting CP to CV is:

Show that equation B of example 6.2 is another form of this expression.

What is the result of application of this equation to an ideal gas ?
b.) Heat capacities CP and CV are defined as temperature derivatives respectively of U and H. Because these properties are realted, one expects the heat capacities also to be related. Show that the general expression connecting CP to CV is:

Show that equation B of example 6.2 is another form of this expression.
HW #1, 6.41 - Problem title here- 8 pts
Starting from Eqn (*) in the class handout from lecture #3,
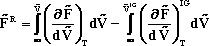
derive the equation for the Helmholtz Free Energy in Eqn (**) of the same handout.
Show all your work and explain every step of the derivation.
HW #1, 6.49 - Enthalpy and Entropy Changes of Vaporization - 12 pts
From data in the steam tables:
a.) Determine values for Gliq and Gvap for saturated liquid and vapor at 150 psia. Should these be the same ?
b.) Determine values for DHvap / T and DSvap at 150 psia. Should these be the same ?
c.) Find values for VR, HR, and SR for saturated vapor at 150 psia.
d.) Estimate a value for dP*/dT at 150 psia and apply the Clapeyron Equation to evaluate DSvap at 150 psia. Does this result agree with the steam table value ?
e.) Use the SRK EOS to evaluate VR, HR, and SR for saturated vapor at 150 psia. Do these results agree with the values you found in part [c] ?
a.) Determine values for Gliq and Gvap for saturated liquid and vapor at 150 psia. Should these be the same ?
b.) Determine values for DHvap / T and DSvap at 150 psia. Should these be the same ?
c.) Find values for VR, HR, and SR for saturated vapor at 150 psia.
d.) Estimate a value for dP*/dT at 150 psia and apply the Clapeyron Equation to evaluate DSvap at 150 psia. Does this result agree with the steam table value ?
e.) Use the SRK EOS to evaluate VR, HR, and SR for saturated vapor at 150 psia. Do these results agree with the values you found in part [c] ?
HW #1, 6.54 - Enthalpy, Entropy and Molar Volume of Ideal Gases - 12 pts
Estimate the molar volume, enthalpy and entropy for n-butane as a saturated vapor and as a saturated liquid at 370 K. The enthalpy and entropy are set equal to zero for the ideal gas state at 101.33 kPa and 273.15 K. The vapor pressure of n-butane at 370 K is 1435 kPa.
HW #1, WB.2 - Production of Acetylene from Calcium Carbide and Water - 15 pts
Five mole of calcium carbide is combined with 10 mol of liquid water in a closed, rigid, high-pressure vessel of volume 750 mL. Acetylene gas is produced by the reaction:
CaC2(s) + 2 H2O(l) => C2H2(g) + Ca(OH)2(s)
Initial conditions are 25oC and 1 bar, and the reaction goes to completion. For a final temperature of 125oC, determine
a.) The final pressure
b.) The heat transferred
At 125oC, the molar volume of Ca(OH)2 is 33.0 mL/mol. Ignore the effect of any gas present in the vessel initially.
CaC2(s) + 2 H2O(l) => C2H2(g) + Ca(OH)2(s)
Initial conditions are 25oC and 1 bar, and the reaction goes to completion. For a final temperature of 125oC, determine
a.) The final pressure
b.) The heat transferred
At 125oC, the molar volume of Ca(OH)2 is 33.0 mL/mol. Ignore the effect of any gas present in the vessel initially.
HW #1, 6.62 - Real and Ideal Work from the Isentropic Expansion of Ethane in a Turbine - 12 pts
A stream of ethane gas at 220oC and 30 bar expands isentropically in a turbine to 2.6 bar. Determine the temperature of the expanded gas and the work produced if the properties of ethane are calculated by:
a.) The ideal gas EOS
b.) The SRK EOS
a.) The ideal gas EOS
b.) The SRK EOS
HW #1, WB3 - Molar Volume of a Real Gas Mixture - 12 pts
An equimolar mixture of methane and propane is discharged from a compressor at 5500 kPa and 90oC at the rate of 1.4 kg/s. If the velocity in the discharge line is not to exceed 30 m/s, what is the minimum diameter of the discharge line ?
Subscribe to:
Comments (Atom)